什么是弗劳恩霍夫衍射和菲涅尔衍射(Fraunhofer and Fresnel Diffraction)?
发布时间:2023-09-26 10:05:21 阅读数: 559
光的衍射是指光波在遇到材料边缘或通过狭缝时发生弯曲或扩散的现象。光在电磁场中表现得像量子化的波。当它传播时,也会出现内部衍射。内衍射是指光波与衍射物体或孔径相互作用,导致偏离直线路径。产生这种现象的原因是光不断与自身相互作用,导致不同波段之间产生内部干涉。因此,光波会弯曲或扩散。这就形成了一种独特的明暗区域图案,即衍射图样。这种衍射图样可以在障碍物或光圈后面的屏幕上观察到。弯曲的程度取决于狭缝的直径。它还受多个因素的影响,包括波的大小、形状和波长。弗劳恩霍夫衍射和菲涅尔衍射是光波与障碍物或光圈相互作用时产生的两种不同形式的衍射。

图 衍射图样
衍射产生具有明暗条纹的干涉图案。由于来自狭缝各部分的建设性干扰,中央最大值的强度最高。从中心最大值向四周移动,由于来自狭缝不同部分的破坏性干扰增加,条纹强度降低。次级最大值出现在特定角度,来自狭缝特定部分的建设性干扰。连续的亮条纹强度会进一步降低。
菲涅尔衍射
菲涅尔衍射是指光波在有限距离内遇到障碍物或穿过光圈的现象。当衍射物体、光源和观测平面之间的距离与光的波长相当时,就会出现这种现象。19 世纪初,法国物理学家奥古斯丁-让-菲涅尔(Augustin-Jean Fresnel)首次观察到并描述了菲涅尔衍射。
当一束相干光穿过一个小孔或绕过一个与光波长大小相当的障碍物时,就会产生衍射。当光线穿过小孔或绕过障碍物时,波面会相互干涉,导致光线散开并偏离原来的路径。这种波面干涉产生了一种独特的图案,称为菲涅尔衍射图样。这种图案可以观察到明亮和暗淡的条纹区域,分别代表建设性和破坏性干涉。在建构干涉较强的区域,由于波的叠加产生了放大的强度,条纹显得更亮。相反,在有破坏性干涉的区域,由于干涉波相互抵消,导致强度减弱,因此表现出较暗的条纹。
在菲涅尔衍射中,入射波面和出射波面都是球面或圆柱面。考虑到整个波面的曲率和振幅变化,会产生复杂的干涉图案和光波弯曲。干涉图案的复杂性源于波阵面上不同相位、振幅和空间分布的波的复杂叠加。
由此产生的干涉图案会在一定距离的屏幕上产生一系列明暗相间的条纹。条纹的强度与屏幕上某一点干涉波的振幅直接相关。
在菲涅尔衍射图样的中心最大值(最大值)处,来自整个孔径的所有小波相位相加,形成建设性干涉。这导致图案中心出现明亮的条纹。
当我们从中心最大值向明亮的边缘移动时,二次光源(来自光圈上不同点的小波)到屏幕上观察点的路径长度略有不同。这些路径长度差异会导致小波之间的相位差异。在某些区域,小波可能会发生建设性干涉,从而产生亮条纹,而在其他区域,小波可能会发生破坏性干涉,从而产生暗条纹。
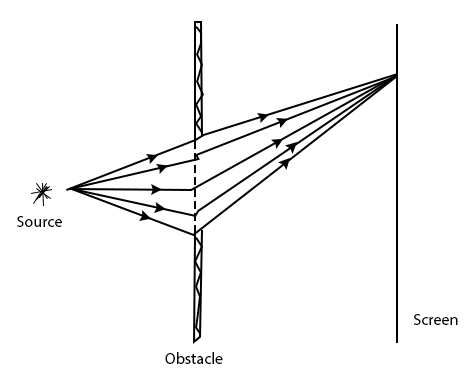
图 菲涅尔衍射
在距离光圈或障碍物一定距离的地方放置一块屏幕,让衍射光落在屏幕上,就可以观察到菲涅尔衍射产生的衍射图样。衍射图样由圆形明暗条纹组成,随着与光圈或障碍物距离的增加,条纹逐渐变宽(单个条纹之间的间隔或间距增加)。
菲涅尔利用叠加原理和惠更斯原理来解释这种现象。惠更斯原理指出,波阵面上的每个点都会产生次级波,而正是这些次级波的干涉导致了衍射。干涉在任何一点都会产生光的强度。

图 惠根原理
在菲涅尔衍射中,衍射图样通常由圆形的明暗条纹组成,也称为菲涅尔区或环。这些区域是根据波面上相邻点之间的路径长度差(从孔径到观察点的测量值)来定义的。路径长度差决定了到达这些相邻点的波之间的相位差,这种相位差会导致建设性或破坏性干涉。
菲涅尔第一区是最靠近光圈的区域,波阵面上相邻点之间的路径长度差为零或波长的整数倍。在这一区域,到达相邻点的波相位一致,产生建设性干涉,观察到明亮的条纹。
随着我们从第一区域向外移动,路径长度差逐渐增大,到一定距离时,路径长度差等于波长的一半。在这个距离上,到达相邻点的波长相差半个波长,从而产生破坏性干涉,出现暗色条纹。
第二个区域从路径长度差为半个波长的地方开始,一直延伸到路径长度差为一个波长的地方,在这里由于建设性干涉形成了第二个亮条纹。这种模式一直持续到每个连续区域的亮暗条纹交替出现。
衍射波的强度取决于菲涅尔区波面之间的干涉程度。如果光圈或物体较小,区域就会较窄,干涉就会较强,从而产生较明显的衍射图样和锐利的条纹。反之,如果光圈或物体较大,则区域较宽,干涉较弱,衍射图样不明显,条纹较宽。
菲涅尔衍射产生的衍射图样的强度可以用菲涅尔-基尔霍夫衍射积分来计算: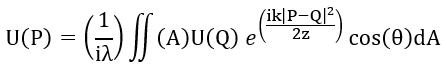
其中 U(P) 是屏幕上 P 点衍射光的复振幅,U(Q) 是光圈或障碍物上 Q 点入射光的复振幅,λ 是入射光的波长,k 是波数 (2π/λ)、 z 是光圈或障碍物与屏幕之间的距离,|P-Q| 是点 P 和 Q 之间的距离,θ 是光圈或障碍物的法线与衍射光方向的夹角。
菲涅尔衍射的光栅方程将入射光的波长与狭缝间的距离和屏幕上亮条纹的位置联系起来。它可以表示为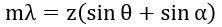
其中,m 是亮条纹的阶数,λ 是入射光的波长,z 是狭缝与屏幕之间的距离,θ 是入射光束与光栅法线之间的夹角,α 是衍射光束与光栅法线之间的夹角。
该公式表明,亮条纹的位置取决于入射光的波长、狭缝与屏幕之间的距离以及入射角和衍射角。通过调整这些参数中的任何一个,都可以操纵亮条纹的位置。
菲涅尔衍射的应用
菲涅尔衍射的应用多种多样,横跨多个科学和工程领域。菲涅尔衍射在光学中被用于制造各种透镜和光学设备,在声学和电磁波中也有应用。此外,菲涅尔衍射还应用于衍射层析成像、粒子尺寸测量、显微镜和全息摄影。
对菲涅尔衍射的理解在现代光学的发展中发挥了重要作用,并为创造创新的光学设备(如菲涅尔透镜、衍射光栅和全息透镜)铺平了道路。
在光学仪器中,衍射光栅用于分散和分析光线。
在光学显微镜中,菲涅尔衍射用于研究细胞或细菌等小物体产生的衍射图样。
这种衍射用于通过专门设计的孔径或透镜来塑造激光束。
菲涅尔衍射还可用于无线电通信,分析无线电波在障碍物周围衍射时的行为。
它还可用于全息技术,以创建三维图像。
夫琅和费衍射
弗劳恩霍夫衍射是一种特殊类型的衍射,当光波穿过光圈或遇到无限远的障碍物时就会发生这种衍射。在这种衍射中,观测点位于远场区域,距离光圈或物体相对较远,因此传入和传出的光波实际上是平面的。由于光源位于无限远处,通过狭缝的光线是平行光线。为了使这些平行光线聚焦在屏幕上,需要使用会聚透镜。它是以德国物理学家约瑟夫-冯-弗劳恩霍夫(Joseph von Fraunhofer)的名字命名的,他在 19 世纪初首次观察到这一现象。
当一束光入射到比光的波长小得多的狭缝或一系列狭缝时,就会产生弗劳恩霍夫衍射。衍射量受孔径或狭缝相对于光的波长的大小的影响。
当光线通过狭缝时,会发生衍射,即在狭缝边缘扩散和弯曲。这些来自狭缝不同点的衍射光会相互干涉,在一定距离外的屏幕上形成干涉图案。衍射图样是穿过狭缝边缘的衍射波与直接穿过狭缝的非衍射波相互干涉的结果。
衍射图样的特征是一系列与狭缝平行的明暗条纹。条纹的位置取决于入射光的波长、狭缝和屏幕之间的距离以及狭缝的宽度。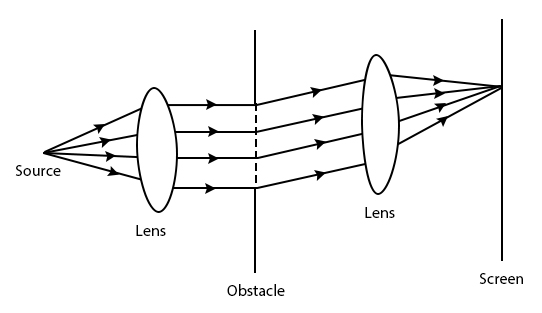
图 弗劳恩霍夫衍射
弗劳恩霍夫利用傅立叶变换原理解释了衍射图样。他指出,通过对复杂物体的振幅透射函数进行傅里叶变换,可以得到该物体的弗劳恩霍夫衍射图样方程。振幅透射函数是一种数学函数,用于描述透明光圈或物体如何影响通过它的光的振幅。
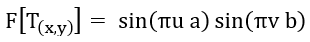
u 和 v 分别是对应于 x 和 y 方向的空间频率变量。
傅立叶变换是一种数学运算,它将一个复杂函数拆分成一组较简单的函数,即频率分量,这些频率分量可以形象地表示为一系列干涉条纹。通过对振幅透射函数进行傅里叶变换,弗劳恩霍夫能够计算出物体衍射光的空间强度分布。
屏幕上衍射光的空间强度分布(I(x, y))是通过求傅里叶变换的平方大小得到的:
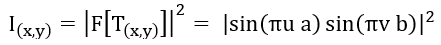
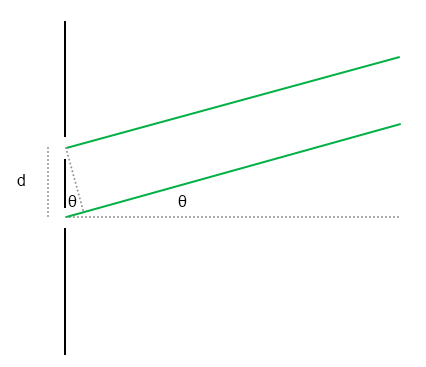
弗劳恩霍夫衍射所产生的衍射图样的强度可以通过以下公式计算出来:
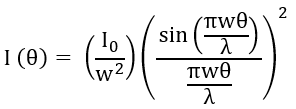
其中,I0 是入射光束的强度,w 是狭缝的宽度,λ 是入射光的波长,θ 是衍射图样中心与所考虑的条纹之间的夹角。
与弗劳恩霍夫衍射有关的另一个重要方程是光栅方程,它将入射光的波长与狭缝之间的距离和亮条纹的位置联系起来:
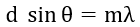
其中,d 是狭缝之间的距离,θ 是入射光方向与衍射光方向之间的夹角,λ 是入射光的波长,m 是亮条纹的阶数。
夫琅和费衍射的应用
夫琅和费衍射是物理学中的一种基本现象,在光学、物理学、化学和材料科学等各个领域都有许多实际应用。它是一种强大的工具,使科学家和工程师能够分析光和其他波(如 X 射线和声波)的特性。这些信息应用广泛,从 X 射线晶体学到激光技术,从天文学到显微镜。
在光学光谱学中,弗劳恩霍夫衍射可用于分析光的光谱成分。
X 射线穿过晶体时产生的菲涅尔衍射图样可用于确定晶体结构。
在天文学中,它用于分析恒星和星系的光谱。
在激光技术中,弗劳恩霍夫衍射用于塑造和控制激光的输出光束。
为了确定小颗粒(如气溶胶中的颗粒)的大小,则使用菲涅尔衍射法。
弗劳恩霍夫衍射与菲涅尔衍射的区别
弗劳恩霍夫衍射与菲涅尔衍射的主要区别在于衍射物体与观察衍射图样的屏幕之间的距离。在夫琅和费衍射中,衍射物体远离屏幕,因此衍射图样的数学分析较为简单。与此相反,菲涅尔衍射法是将衍射物体放置在离屏幕较近的地方,从而产生更复杂的衍射图样,这种衍射图样取决于物体与屏幕之间的距离。另一个区别是衍射物体或孔径的大小。
| 菲涅尔衍射 | 弗劳恩霍夫衍射 |
| 球形或圆柱形波面发生衍射 | 平面波面发生衍射 |
| 光波来自有限距离的光源 | 光波来自无限远处的光源 |
| 难以观察和分析 | 易于观察和分析 |
| 不使用透镜 | 使用凸透镜 |





