光操纵的突破:揭示新的有限势垒束缚态

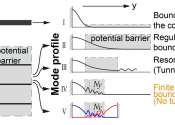
图1所示。与直觉相反，如图IV和V所示，一种状态完全被厚度有限且非常小的带隙材料所捕获。学分:光:科学与应用(2024)。DOI: 10.1038/s41377-024-01417-1

探索波在各种介质中的传播和定位一直是光学和声学研究的核心焦点。具体来说，在光子学和声子学中，科学家们一直致力于理解和控制周期性介质中光波和声波的行为。

光子晶体具有独特的带隙特性，为研究波的传播和定位提供了良好的平台。这些由晶体周期性结构引起的带隙可以控制波的传播，甚至在一定频率范围内完全抑制波。传统上，人们认为光子晶体的边界模式受晶体尺寸(点阵位数)的强烈影响。一般认为这些模态在大系统(有许多点阵位)中更容易受限，因为隧穿的概率随着系统尺寸的增加而显著降低。这种现象对于设计和实现高性能光子器件，特别是追求器件的高集成度和小型化至关重要。

此外，在光子晶体研究中，连续介质中的束缚态(BICs)也引起了人们的关注，因为它们揭示了即使在连续光谱中，某些独特的模式也可以被限制在特定的区域内。这一现象为认识和控制光波的局域化提供了新的视角。它在实际应用中显示出巨大的潜力，如提高光学器件的性能和效率。

发表在《光:科学与应用》上的一项新研究提出并证实了有限势垒束缚态的存在。系统的谱通常由连续和离散谱组成(图1左面板)。传统观点认为，束缚态的特征值谱是离散的，而非束缚态的特征值谱是连续的。

例如，在电子系统中，如果粒子的能量低于无穷远处的势能，则该状态被一个离散谱束缚;而能量高于势能的粒子散射，形成连续谱。

对于光波和声波，离散状态的形成是由于屏障施加的边界条件，例如“带隙”。这些离散状态可以在理想条件下完全局部化(无限势垒宽度，图1- 2)。然而，当势垒宽度有限时，态有可能隧穿势垒，成为共振态(图1-III)。

值得注意的是，连续介质中的束缚态(bic)在空间上被束缚在连续光谱的能量/频率范围内(图1- 1)。本研究引入了一个与bic平行的反直觉概念:某些态可以完全束缚在非常薄的带隙材料中，使它们无法通过带隙材料隧穿(图1-IV和1-V)。

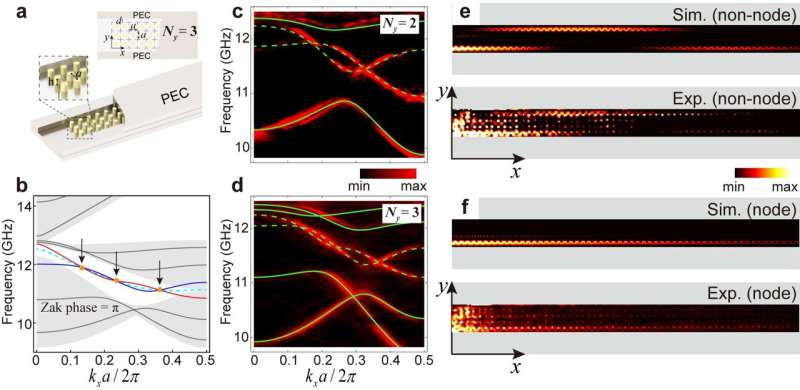
图2所示。a、Ny=3时的实验设置说明。b, Ny=3时的能带结构(灰色区域为投影能带结构)。c-d，分别为Ny= 2和3的实测(色码)和模拟(线)波段结构。e-f, y= 4在非节点频率和节点频率下的模拟电场分布和实验电场分布。学分:光:科学与应用(2024)。DOI: 10.1038/s41377-024-01417-1

该研究首先展示了一种特殊的镜面对称光子晶体带结构，可以很好地控制边界模式的跃迁。当光子晶体的宽度(沿y方向的点阵位数，Ny)较小时，两侧的边界模式相互作用并分裂为奇偶模式(图2 a-d)。在特定波矢量(节点)处，边界模的耦合强度为零。即使光子晶体的宽度(Ny)很小，边界模式也不能从光子晶体的一边跳到另一边(图2 e-f)。一般认为，为了抑制边界模的耦合，需要许多点阵位。然而，这项研究挑战了这一观点，为在微观尺度上操纵光子行为开辟了一种新的方法。

在之前的结构之后，研究人员移除了光子晶体的一个PEC边界，揭示了一个新的结构。他们发现，在特定节点波矢量上的剩余边界模式完全被捕获，形成连续体(fbic)中的有限势垒激活束缚态。

由于两种边界模式的解耦，这些fbic表现出非辐射特性。在边界模式耦合强度为零的节点上，去掉一侧PEC存在一个辐射系数为零的状态，且其频率与双PEC场景中的节点频率相匹配，从而确定其为FBIC。

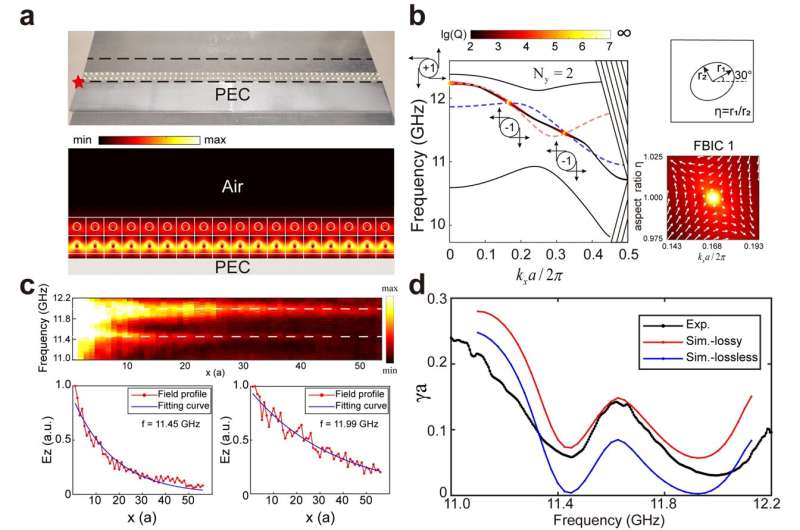
图3所示。a，当Ny= 2时，样本在节点波矢量处的本征场振幅分布的照片。b、Ny= 2时的能带结构、相应的边界模Q因子、几何参数η的定义和FBIC的拓扑特性。c-d，第二种结构中边界模式的场分布和衰减特性。学分:光:科学与应用(2024)。DOI: 10.1038/s41377-024-01417-1

此外，通过将圆形介质改变为椭圆形以打破原有的镜面对称性，并引入新的几何参数η，在kx-η参数空间中定义了圈数，揭示了fbic的拓扑特征，并确认了这些模式为BICs(图3 a - b)。考虑到微波频率下不可避免的介电损耗，本研究通过测量边界模式的衰减(图3 c-d)实验验证了边界模式，证明了边界模式在极少数晶格点(Ny= 2,3等)内完全定位，为实现边界模式提供了一种新的方法。

这项开创性的研究探索了光子晶体中的新物理现象，并实现了边界模式的精细控制。本工作不仅从理论上对光子晶体中边界模式的隧穿和束缚提供了新的认识，而且通过微波实验证实了边界模式在特定波矢量上的完全局域化，为光子学领域带来了新的视角。

该研究揭示了操纵光子行为的新方法，对开发高集成度光子器件具有重要意义。它还提供了利用光子晶体增强光-物质相互作用的新策略，有可能在非线性光学和光与二维材料之间的相互作用方面取得突破。这些发现可能会启发未来的研究，例如将这些原理应用于其他波系统，如声子晶体。