传统技术与深度学习的协同作用实现了单帧高精度条纹模式分析

光学计量是一种通用计量技术，它以光为信息载体进行非接触和无损测量，是制造、基础研究和工程应用的基础。

随着激光和电荷耦合器件（CCD）的发明，许多光学计量方法和仪器因其在精确度、灵敏度、可重复性和速度方面的优势，被广泛应用于最先进的制造工艺、精密定位和质量评估中。

对于许多光学计量技术，如干涉测量法、数字全息法和条纹投影轮廓测量法（FPP），条纹图案分析是从记录的条纹图案中恢复基本相位分布的主要研究重点。要动态重建物体的各种所需物理特性（轮廓、距离、应变等），从条纹图案中检索相位的准确性和效率至关重要。

对于基于 FPP 的结构光三维成像，为了最大限度地减少单次重建所需的条纹数量，南京理工大学陈谦教授和左超研究小组建立了移相轮廓测量和时相解包的理论框架，并开发了一系列用于快速三维测量的复合移相方法，包括双频移相、2+2 移相、基于几何约束的复合移相和微傅里叶变换轮廓测量（μFTP）。

这些复合相移方法将每次三维重建所需的条纹图案数量从约 10 个减少到 5 个、4 个、3 个甚至 2 个，从而实现了每秒 10k 帧的高速三维传感。

尽管如此，只用一个图案就能实现高精度三维重建一直是结构光三维成像技术不断追求的终极目标。然而，FTP 成功的关键在于，物体表面调制的高频条纹信息能在频域上与背景强度很好地分离。

因此，FTP 技术仅限于测量高度变化有限的光滑表面。

最近，随着可用数据和计算资源的爆炸式增长，深度学习作为一种 "数据驱动 "的机器学习技术，在计算机视觉和计算成像等众多领域取得了令人瞩目的成就。深度学习几乎渗透到光学计量学的方方面面，为许多具有挑战性的问题提供了解决方案，如边缘去噪、边缘分析和数字全息重建。

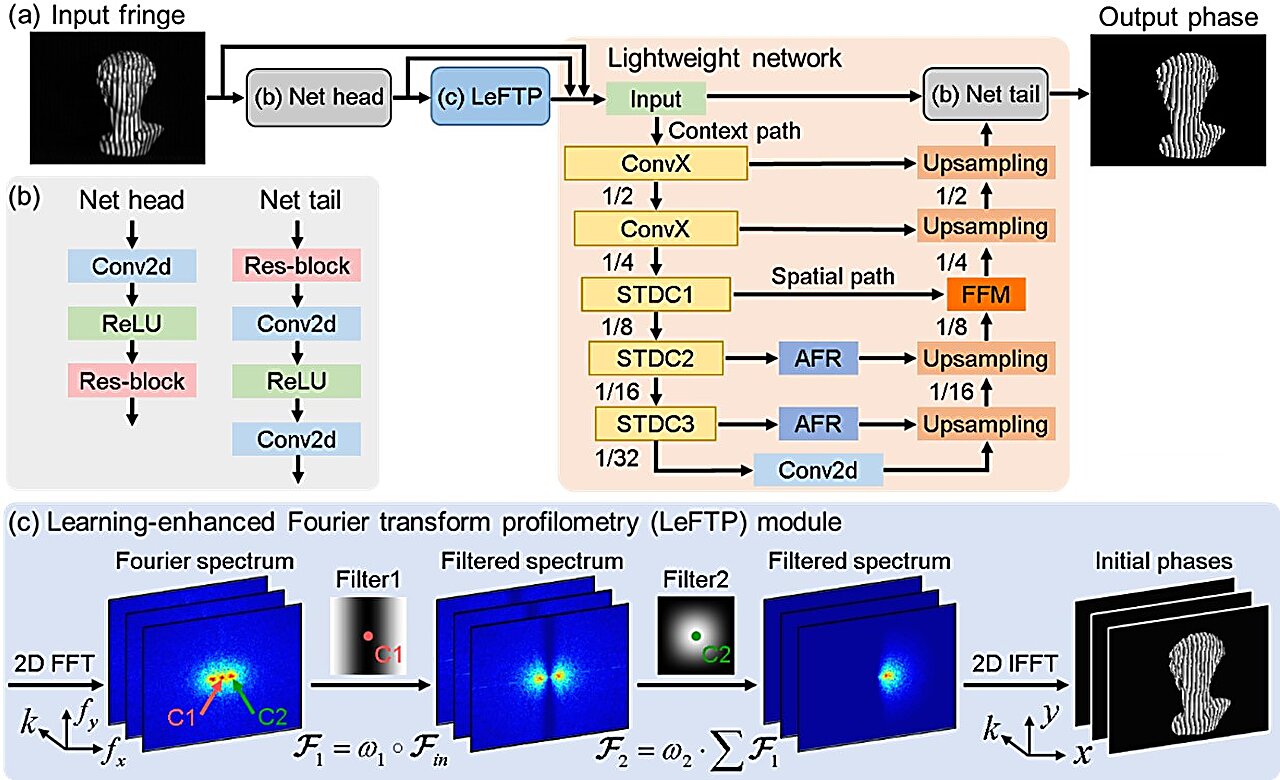
图 2. 拟议的 PI-FPA 概述。(a) PI-FPA 包括一个 LeFTP 模块和一个轻量级网络，(b) 网头和网尾，(c) LeFTP 模块的相位检索过程。来源：Opto-Electronic Advances (2023)。DOI: 10.29026/oea.2024.230034

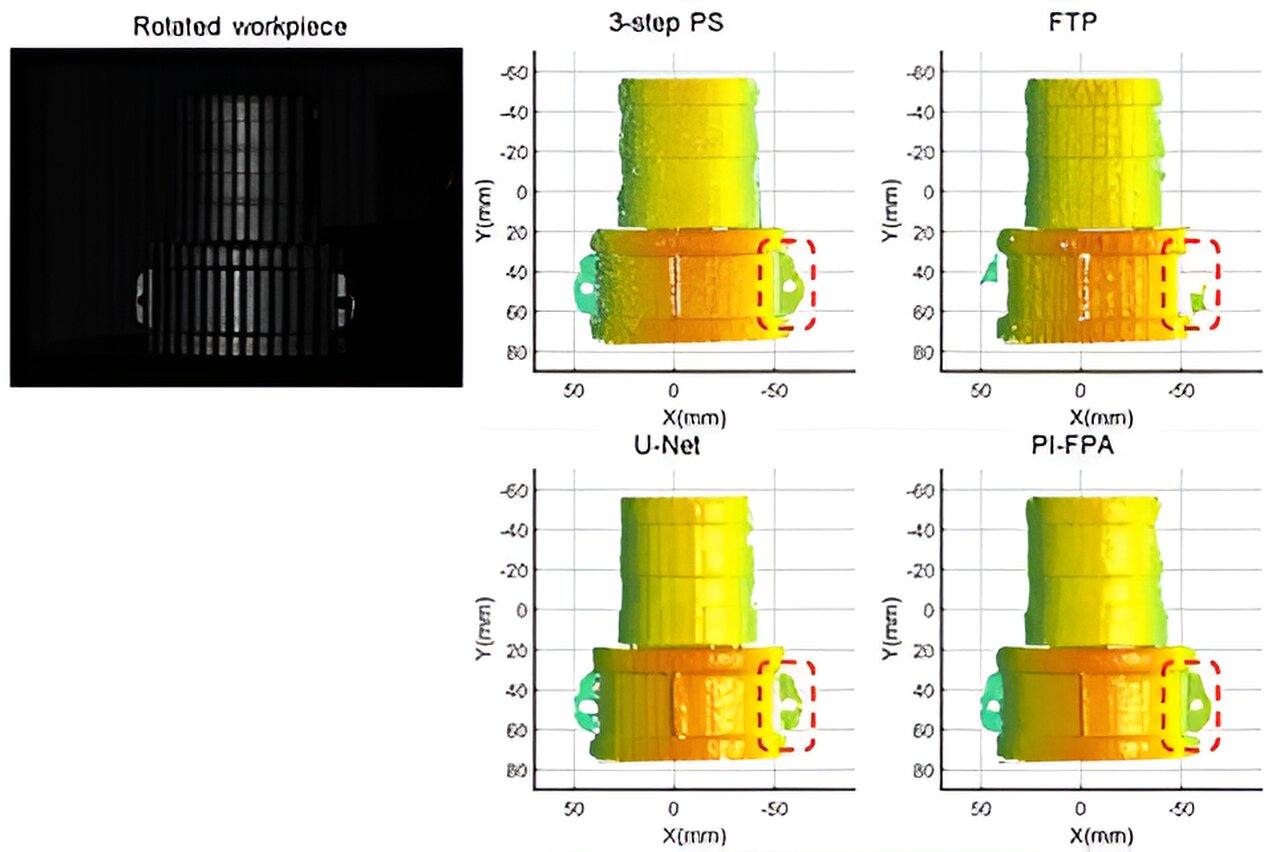
图 3. 用不同的条纹分析方法（包括三步 PS、FTP、U-Net 和 PI-FPA）对工件模型进行 360 度动态三维重建的结果。来源：Opto-Electronic Advances (2023)。DOI: 10.29026/oea.2024.230034

然而，与传统的边缘分析方法不同，这些深度学习方法主要侧重于训练 DNN，以便从海量输入和输出数据对中准确识别图像到图像的变换，因为在当前的深度学习实践中，图像形成的物理规律或与测量有关的其他领域专业知识尚未得到充分利用。

因此，深度学习方法在解决复杂物理问题时的性能在很大程度上依赖于数据集的基本统计特征。为了在速度、准确性、可重复性和泛化方面突破边缘模式分析的极限，基于物理学的传统方法和数据驱动的学习方法的协同作用已成为大势所趋[图 1(b)]。

南京理工大学陈谦教授和左超教授课题组在《光电子学进展》（Opto-Electronic Advances）上发表了一篇论文，报告了一种基于物理学的边缘模式分析深度学习方法（PI-FPA），该方法将轻量级 DNN 与学习增强型傅立叶变换轮廓测量（LeFTP）模块集成在一起[图 2]，实现了更精确、计算效率更高的单次相位检索。

与通用的端到端图像变换网络（U-Net 及其衍生物）相比，轻量级网络能以较低的计算成本完善初始相位，从而进一步提高相位精度。

不同条纹分析方法对工件模型进行 360 度动态三维重建的结果如 [图 3] 所示。

对于三步 PS 方法，在测量动态场景时，物体与连续投射的相移条纹图案之间的相对运动会造成运动伪影，从而给三维重建结果带来不可忽略的误差。

对于单帧条纹分析，FTP 适用于动态三维测量，但由于频谱重叠，会产生精度和分辨率较低的粗糙三维结果。

U-Net 可以进一步提高三维重建的质量，但它无法可靠地获取训练数据集中相对较少的金属材料物体的相位，从而无法恢复精细表面。该实验证明，所提出的 PI-FPA 可用于复杂结构零件的高质量、高效率三维建模。

所提出的用于条纹模式分析的物理信息深度学习技术（PI-FPA）不仅能像传统神经网络一样学习数据集内固有的统计特征，还能掌握描述图像形成的物理规律，实现高精度、高计算效率的单帧相位重建，同时对网络从未见过的稀有样本也表现出良好的泛化能力。

未来，研究团队将研究 PI-FPA 在不同类型条纹图像中的相位恢复性能，并探索相关条纹分析在光学计量学中干涉测量和数字全息领域的应用，进一步突破条纹模式分析在速度、精度、可重复性和泛化方面的极限。

参考资料

Wei Yin et al, Physics-informed deep learning for fringe pattern analysis, Opto-Electronic Advances (2023). DOI: 10.29026/oea.2024.230034