什么是衍射光栅(Diffraction Grating)?
发布时间:2023-05-22 08:00:00 阅读数: 799
衍射光栅是一种利用多个均匀分布的狭缝产生的衍射图案的装置。它由一个不透明的屏幕组成,上面有几个等距的狭缝。当光线通过衍射光栅上的每条狭缝时,会发生衍射,并被分散成多个光束,这些光束相互干扰和重叠,产生一个独特的明暗带图案,称为衍射图案。图1显示了一个使用衍射光栅的装置。
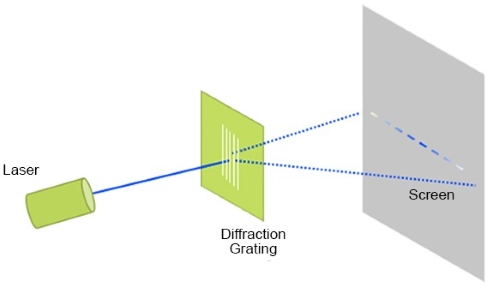
图1:使用衍射光栅的装置
在实践中,透明的片子被用来创建一个衍射光栅,用一个钻石点在它上面划出平行的沟槽,在电子控制机制的帮助下操作。这些凹槽作为不透明的区域发挥作用。高质量的光栅每厘米可以有多达10,000个缝隙,光栅的尺寸可以达到50 x 75平方厘米。实现这样的精度对光栅技术来说是至关重要的。而且,市面上的光栅都是原始尺码表面的塑料复制品。使用衍射光栅的光的衍射情况如图2所示。
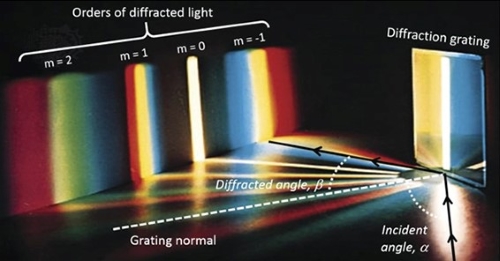
图2:使用衍射光栅的光衍射
当波长为λ的平面光波正常入射到衍射光栅上时,在另一侧形成的主最大值的位置可以通过公式确定:
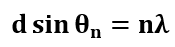
这种关系被称为光栅方程,通过观察n阶最大值的角度θn来计算波长λ。光栅元素d是一个固定的几何常数。如果光源包含多个波长,角度θn随λ变化。然而,对于所有波长,零阶最大值发生在θn = 0。不同波长的高阶最大值几乎被光栅分开。因此,通过测量各种颜色的衍射角,我们可以确定其相应的波长。
自由光谱范围
在多色光源的情况下,有可能在一个特定的位置θ,两个或多个不同波长的最大值重叠,导致:
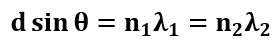
为了确定n阶和(n+1)阶的最大值之间没有重叠的光谱范围(即波长范围),考虑相应的最短和最长的波长,分别为λ1和λ2。形成n阶最大值的最大角度是由于最长的波长λ2。
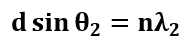
而且,由于最短的波长λ1,形成(n+1)阶最大值的最小角度:
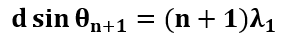
如果θn+1大于或等于θn,那么第n个和第(n+1)个阶次的最大值之间就不会有重叠。平等条件代表了极限情况,在这种情况下:
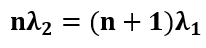
或者
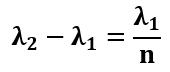
λ2和λ1之间的差值被称为光栅的自由光谱范围,它随着阶数n的变化而变化,在高阶时更小。
光栅的色散
色散是指不同波长的角度分离。光栅的角度色散是通过对光栅方程dsinθn = nλ的微分来定义的,即:
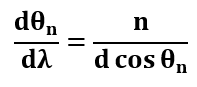
将光栅方程与上述方程结合起来,可以得到、
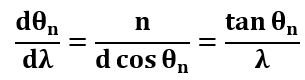
根据定义,光栅的角色散实际上与光栅元件d无关。然而,它随着θn的增加而迅速增加,导致在较高的衍射角下,不同波长之间的角分离较大。
当θn较小时,即cosθn=1时,可以证明(dθn/dλ)=n/d是常数。这种类型的光谱被称为正常光谱,两个波长之间的角距离dθ与它们之间的差异dλ成正比。
光栅的解像力
光栅的分辨力是衡量其分离紧密间隔的波长并产生明显的最大峰值的能力。在数学上,它可以被定义为:
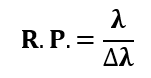
其中Δλ是可以分辨的最小波长间隔。因此,∆λ的值越小,意味着光栅的分辨力越强。
分辨率的极限是由瑞利标准决定的,该标准指出,如果(λ+∆λ)的最大值落在波长λ的第一个最小值上,那么两个波长λ和(λ+∆λ)可以被认为是刚刚解决。
(λ+∆λ)的第n阶最大值的位置可以表示为θn,它满足方程式的要求:
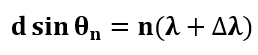
因此,这两个波长可以被解决,如果
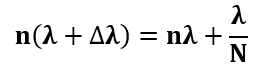
或者
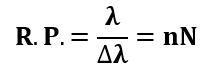
因此,光栅上的狭缝数N与光栅的分辨力有线性关系。另外,对于高阶的光谱,其分辨力也更大。
衍射光栅的应用
衍射光栅通常用于光谱学,将光分离成其组成波长。这可用于研究材料的组成,例如在天文学中,分析来自恒星的光以确定其化学组成。
它们被用于激光技术,以产生具有非常特定波长的激光束。它在电信中很有用,光纤电缆使用激光器来传输数据。
这些光栅可用于产生全息图像,方法是将激光束分开,用一部分照亮一个物体,而另一部分作为参考光束。这两束光之间的干涉图案产生了物体的全息图像。
衍射光栅也被用于望远镜中,以研究来自天体的光线。天文学家可以通过分析光的光谱来确定恒星和星系的组成和温度。
它们可用于光通信,以分离不同波长的光,使多个信息通道可以在一根光缆上同时传输。